堆与堆排序是算法学习中的一环。堆排序如果单从代码量的角度来看是十分简单的，但实际上涉及很多理论部分。虽然网络里关于堆排序的资料非常多，但大多都只按照代码来演示排序过程而已，对具体的原理和许多值得探讨的点都没有深入。如堆是如何调整结构、Floyd 算法为什么产生了实质性的优化等问题。因此写下此文，记录下学习过程的所有疑惑的点以及思考的结果，以供自己日后参考。

主要参考资料为清华大学邓俊辉老师的教材以及维基百科。如有错漏，恳请指正。

概述

维基百科对堆排序 (heap sort) 的解释：

heapsort 是计算机领域中的一种基于比较的排序算法，可视作 选择排序 的优化实现。堆排序与选择排序的相似之处在于同样把输入数组分为已排序和待排序两个区域，并反复执行从待排序区域抽出最大值插入到已排序区域的操作，从而不断缩小待排序区域。它们之间的不同点在于获取待排序区域最大值的方式，堆排序没有把时间浪费在对待排序区域的线性扫描，而是使待排序区域保持堆的结构，从而大幅缩短每一步中获取最大值的耗时。

可以看出，堆排序算法的核心在于使待排序区域维持堆的结构，这也是算法名称的由来。那么什么是堆呢？

二叉堆

堆是一种与二叉搜索树 (Binary Search Tree, BST) 逻辑结构相同的数据结构，即同样由父节点、左右子节点组成。它们之间的不同点在于 BST 显式维持了一个全序结构，而堆则是维持一个偏序结构。

堆中每个父节点与其左右节点中，父节点的值为最大值或最小值，此即为堆序性，相应的堆也被称为最大堆或最小堆。

更准确地说，堆排序算法中使用的是完全二叉堆，与完全二叉树 (Complete Binary Tree) 逻辑结构完全相同。

由堆序性的定义不看看出，二叉堆的根节点为整个集合的最大值（最大堆）或最小值（最小堆）。由于二者处理逻辑别无二致，因此本文仅讨论最大堆。

元素位置

实际上二叉堆是一种逻辑上的结构，只需要将输入数组的元素位置按层次遍历的方式进行映射即可得到相应的堆结构，而无需像二叉树那样定义节点类（包含节点的值与左右节点的引用）。

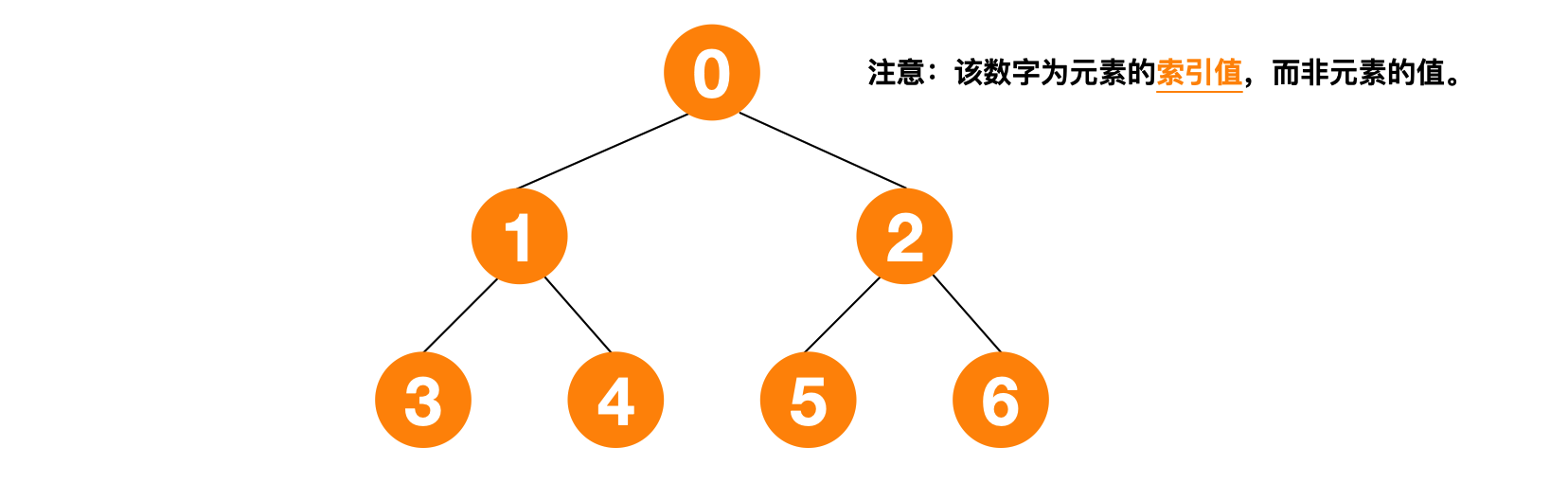
对于输入数组中索引值为 i 的任意元素，其父节点、左节点与右节点的索引值均满足以下规律：

  • 其父节点的索引值为 parent(i)=⌊(i - 1) ÷ 2⌋（向下取整）。如上图索引值为 6 的节点，其父节点的索引值为 2.
  • 其左节点的索引值为 left(i)=(2 × i) + 1. 如上图索引值为 1 的节点，其左节点索引值为 3.
  • 其右节点的索引值为 right(i)=(2 × i) + 2 或 right = left + 1. 如上图索引值为 1 的节点，其右节点索引值为 4.

堆操作

当堆的结构发生变化时，如插入新元素或移除堆顶（根节点），需要重新调整节点位置，才能使得堆的整体满足堆序性、使堆顶仍为最大值。而这种结构性调整可能会引起连锁效应：被交换的节点本身也是一个子节点（或父节点），因此需要递归地调整。

从叶节点一直上溯到根节点，被称为上滤操作；从根节点开始，一直向下交换直到叶节点，被称为下滤操作。

插入元素

  1. 新元素添加在数组的末尾；
  2. 判断新元素与其父节点是否满足堆序性，并进行必要的条件；
  3. 如果第二步发生了节点的交换，则需要继续往上递归，最坏情况会到达堆顶；

移除堆顶

  1. 移除根节点；
  2. 将最后一个节点移至根节点，作为新的根节点；
  3. 判断根节点的堆序性并进行必要的交换；
  4. 如果第三步发生了交换，则需要继续往下递归，最坏情况会到达叶节点；

由此可见，上滤和下滤是互为镜像的操作，且执行次数等于堆的高度 O(logn).

堆排序

堆排序是充分利用了二叉堆的堆序性的排序方式，从整体上看主要步骤分为两步：

  1. 建堆（最大堆化），即将输入的乱序数组转换为偏序的二叉堆；
  2. 依次从堆中取出最大值，插入至有序区域，即可完成排序；

建堆

建堆操作就是将一个无序的数组转化为最大堆的操作，又被称为最大堆化 (max heapification). 操作过程为对输入数组的元素进行逐一扫描，并在扫描过程中不断地调整堆的结构。

显然必须对输入数组的所有元素进行一次扫描才能完成建堆，否则任何遗漏的元素都可能是最大值。由于每个父节点都要与其子节点进行比较，因此在实际的遍历中，扫描到最后一个父元素为止即可。

关于建堆的最关键的问题是顺序问题，即自上往下建堆，还是自下往上建堆？

“向下”的意思是扫描过程从数组索引值较低的元素开始，往索引值高的方向扫描。“向上”扫描则正好相反，从索引值高的元素，即叶节点开始，往索引值小的方向扫描。

这里需要先强调一下，“自上而下” (top-down) 或“自下而上” (bottom-up) 是从建堆的整体过程来看，可以说是堆的增长方向。而“上滤”和“下滤”则为单个节点称为堆的部分后需要调整的方向。前者与后者的方向恰好相反，即“自上而下”地建堆，则每个节点需要“上滤”，而“自下而上”地建堆，则每个节点需要“下滤”。

自上往下扫描的过程可看作将n个待排序元素往二叉堆插入的过程。由于每次插入操作后需要进行上滤操作（次数为 O(logn)），因此自上而下的建堆方式整体的复杂度为 O(nlogn).

自下而上的建堆方式则将乱序的数组视作一个破碎的堆，然后在自下往上的扫描过程中对堆进行修复。

建堆操作最关键的一点是，自下而上的建堆方式实际上只需要 O(n) 次即可完成。与之前算法产生效率差的根本原因是，二叉堆中每一层的节点数都以指数级增长，因此底层的节点数远大于顶层节点数。每层的节点数为 2ᵏ（层数或深度 k 从 0 开始），因此第 10 层的节点数为 1024，比前几层的节点数高出几个数量级。而这些数量庞大、位于堆下层的节点离叶节点更近、离根节点更远。对比自上往下的建堆方式需要上滤至根节点，自下往上的建堆方式下滤至叶节点的方式最终产生了渐进意义上的优化。

由于该方法由 Floyd 提出，因此又称 Floyd 算法。具体推导过程可参考我在知乎上的回答：堆排序中建堆过程时间复杂度O(n)怎么来的？

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/**
 * 堆排序，非线程安全
 * @author Lawrence
 */
public class HeapSort {
    
    public void heapSort(int[] nums) {
        int lastIndex = nums.length - 1; // 数组最后一个元素的索引值
        int lastParent = (lastIndex - 1) / 2; // 最后一个元素对应的父元素索引值
        
        // 自下往上建堆，又被称为最大堆化
        for (int i = lastParent; i >= 0; i--) {
            siftDown(nums, i, lastIndex);
        }
        
        // 将堆顶移至数组右侧，以 i 为边界，左侧为堆，右侧为已排序区域。
        for (int i = lastIndex; i > 0; i--) {
            swap(nums, 0, i);
            siftDown(nums, 0, i - 1);
        }
    }
    
    int left, right, max; // 每次验证堆序性所需的临时变量
    
    /**
     * 对数组中索引值为 {@code index} 的节点进行下滤操作
     * @param nums 原数组（原地排序）
     * @param index 当前节点的索引值，需要判断其是否满足堆序性
     * @param last 标识当前堆边界的索引值
     */
    private void siftDown(int[] nums, int index, int last) {
        boolean changed;
        do {
            changed = false;
            left = (2 * index) + 1; // index 节点的左子节点
            if (left > last) {
                return;
            }
            
            right = left + 1; // index 节点的右子节点
            max = left; // max变量为左右子节点中的较大值
            if (right <= last && nums[right] > nums[left]) {
                max = right;
            }
            
            if (nums[index] < nums[max]) { // 当前节点小于子节点中的较大值，需要进行交换并继续下滤
                swap(nums, index, max);
                index = max;
                changed = true;
            }
        } while (changed);
    }
    
    /**
     * 交换数组中的两个元素
     * @param nums
     * @param i
     * @param j
     */
    public static void swap(int[] nums, int i, int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
}